티스토리 뷰
지난 포스팅 4강에서 순수한 반도체의 전자와 정공의 농도 식으로 다음과 같은 관계식을 얻었습니다.

그리고 이를 Nc와 Nv로 관계식을 변경하면 아래와 같습니다.
(순수한 반도체이므로 ni와 pi는 같습니다.)

이러한 방법을 이용하여 비축퇴 반도체(Non-degenerated Semiconductor)에서도 관계식을 사용할 수 있습니다.


위 관계식은 N-type,P-type에서 모두 같습니다.
다만, N-type이라면 전자의 농도가 높을 것이고, P-type이라면 홀의 농도가 높게나올것입니다.
즉, 이러한 관계가 성립하게 됩니다.

위 식은 이것을 의미합니다.
Conduction Band와 Fermi Level의 에너지 준위차이가 적을 수록
즉, Fermi Level이 높을 수록 ( Ec는 물질마다 고정값) 전자의 농도가 높게 도핑되어있는 상태이고
반대로, Fermi Level과 Valence Band의 에너지준위 차이가 적을 수록
즉, Fermi Level이 낮을 수록 (Ev 역시 물질마다 고정값) 정공의 농도가 높게 도핑되어있습니다.
위 식 대신 이렇게 표현할 수 도 있습니다.

위 식이 의미하는것은 아래와 같습니다.
(N-type)Fermi Level과 Intrinsic Level의 차이가 클수록, 즉 Fermi Level이 높을 수록 전자의 농도가 높고,
(P-type)Fermi Level과 Intrinsic Level의 차이가 적을 수록, 즉 Fermi Level이 낮을 수록 정공의 농도가 높습니다.
※ NP Product
비축퇴 반도체(Non-Degenerated Semiconductor)에서 아래와 같은 관계식이 성립합니다.

위 식을 ni에 대한 식으로 표현을 바꾸어보겠습니다.

그럼 이제 ni의 제곱을 구하기 위해 빨간색 네모박스와 파란색 네모박스를 곱하겠습니다.

위 식의 결과를 잘 기억해주세요.
그럼 이제 n과 p를 나타내는 관계식을 한번 살펴보겠습니다.


ni의 제곱의 값과 결과가 같은것을 알 수 있습니다.
따라서 우리는 아래와 같은 관계식을 얻어 낼 수 있습니다.

※ 불균형으로 Doping된 반도체의 Charge
불균형으로 Doping되어있는 반도체는 전자와 정공도 있지만, Accepter와 Donor 이온들이 존재합니다.
따라서 아래와 같은 관계식을 가지고, 총 전하량의 합은 균형을 이루어 0을 만족해야합니다.

아래 식을 정리하면 아래와 같은 관계를 가집니다.

이제 위 식을 이용하여 전자의 농도와 정공의 농도 구하는 식을 유도해보겠습니다.

근의 공식을 적용하면 다음과 같습니다.
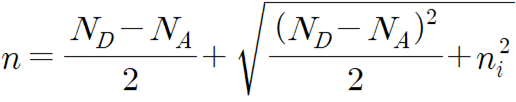
다른 방법으로, 위 식을 p에 관해 정리해보면 아래와 같은 결과를 얻을 수 있습니다.

※ 에너지 준위 수식을 통해 구하는 법
1. 순수 반도체 (Intrinsic Semiconductor) 에너지 준위
순수한 반도체는 전자와 정공의 농도가 같은것을 저희는 알고있습니다.

위 식에서 파란색 박스부분을 풀어주면 Intrinsic 에너지 준위에 대해 구할 수 있습니다.

2. Conduction Band 및 Valence Band와 Fermi level사이의 에너지 준위

위 식을 정리해주면 아래와 같습니다.

'전자공학 > 반도체' 카테고리의 다른 글
| 9강. PN접합의 이해 (PN Junction) (2) | 2019.11.03 |
|---|---|
| 8강. 아인슈타인 관계식 (Einstein Relationship) (4) | 2019.11.02 |
| 7강. 확산전류(Diffusion Current) (1) | 2019.11.01 |
| 6강. 드리프트 전류 (Drift Current)와 반도체 캐리어의 이동도(mobility) (0) | 2019.10.31 |
| 1강. 반도체 소자를 위한 반도체 정의 (0) | 2019.10.26 |
